↓bottom↓

ENERGIA CINETICA RELATIVISTICA

K = E - E₀ = γ·m·c² - m·c² = (γ-1)·m·c²

- - -

Relazione tra energia e quantità di moto relativistica

E² = p²c² + m²c⁴

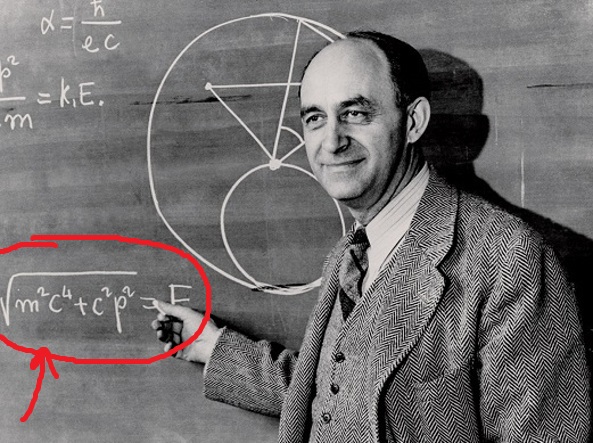ma allora E=mc^2 è sbagliata?!

* è una relazione UTILE

infatti, nella fisica delle particelle elementari la massa NON si può misurare direttamente,

(si pensi alla difficoltà incontrate per calcolare la massa dell'elettrone o del protone,
cfr. L'esperimento di J.J.THOMSON, la misura del rapporto massa-carica di e)

ma la si può calcolare con questa relazione conoscendo energia e quantità di moto della particella

** è un invariante relativistico,

infatti si può scrivere nella forma: (pag.177)

E² - p²c² = (mc)²

E e p possono variare da un riferimento all'altro, ma E²-p²c² è costante in tutti i sistemi di riferimento inerziali

*** ha conseguenze fisiche "sorprendenti"

nella dinamica di Newton, se una particella avesse m=0 avrebbe quantità di moto p=mv ed energia cinetica K=½mv² nulle

nella dinamica relativistica E²=p²c² + m²c⁴ se la massa fosse nulla (m=0) si avrebbe:

E²=p²c²

essendo E=p/v·c², si avrebbe

v=c

e quindi le particelle con massa nulla, possono viaggiare con velocità v=c

NOTA: nel 1926 Gilbert Newton LEWIS battezzerà "FOTONI" i quanti di LUCE

Come si applica La formula di Einstein a basse velocità:

Relazione relativistica tra energia e quantità di moto

↑top↑